0 целых 3 десятичных как пишется

Портал для школьника. Самоподготовка

Что больше десятые или сотые доли. Чтение десятичных дробей

Десятичная дробь в обязательном порядке содержит запятую. Та числовая часть дроби, которая располагается левее запятой, называется целой; правее – дробной:

5,28 5 – целая часть 28 – дробная часть

Дробная часть десятичной дроби состоит из десятичных знаков (десятичных разрядов):

• десятые – 0,1 (одна десятая);
• сотые – 0,01 (одна сотая);
• тысячные – 0,001 (одна тысячная);
• десятитысячные – 0,0001 (одна десятитысячная);
• стотысячные – 0,00001 (одна стотысячная);
• миллионные – 0,000001 (одна миллионная);
• десятимиллионные – 0,0000001 (одна десятимиллионная);
• стомиллионные – 0,00000001 (одна стомиллионная);
• миллиардные – 0,000000001 (одна миллиардная) и т. д.

• прочитать число, составляющее целую часть дроби и добавить слово “целых “;
• прочитать число, составляющее дробную часть дроби и добавить название младшего разряда.

• 0,25 – ноль целых двадцать пять сотых;
• 9,1 – девять целых одна десятая;
• 18,013 – восемнадцать целых тринадцать тысячных;
• 100,2834 – сто целых две тысячи восемьсот тридцать четыре десятитысячных.

Запись десятичных дробей

Чтобы записать десятичную дробь, необходимо:

• записать целую часть дроби и поставить запятую (число, означающее целую часть дроби всегда заканчивается словом “целых “);
• записать дробную часть дроби таким образом, чтобы последняя цифра попала в нужный разряд (при отсутствии значащих цифр в определенных десятичных разрядах они заменяются нулями).

• двадцать целых девять десятых – 20,9 – в этом примере все просто;
• пять целых одна сотая – 5,01 – слово “сотая” означает, что после запятой должны стоять две цифры, но, поскольку в числе 1 нет разряда десятых, он заменяется нулем;
• ноль целых восемьсот восемь тысячных – 0,808;
• три целых пятнадцать десятых – такую десятичную дробь записать невозможно, потому, что в произношении дробной части допущена ошибка – число 15 содержит два разряда, а слово “десятых” подразумевает только один. Правильно будет три целых пятнадцать сотых (или тысячных, десятитысячных и т. д.).

Сравнение десятичных дробей

Сравнение десятичных дробей проводится аналогично сравнению натуральных чисел .

1. сначала сравниваются целые части дробей – больше будет та десятичная дробь у которой больше ее целая часть;
2. если целые части дробей равны, сравнивают поразрядно дробные части, слева направо, начиная от запятой: десятые, сотые, тысячные и т.д. Сравнение ведут до первого несовпадения – больше будет та десятичная дробь у которой будет больше неравная цифра в соответствующем разряде дробной части. Например: 1,28 3 > 1,27 9, т. к. в сотых разрядах у первой дроби стоит 8, а у второй 7.

Десятичная дробь отличается от обыкновенной дроби тем, что знаменатель у нее — это разрядная единица.

Десятичные дроби выделены из обыкновенных дробей в отдельный вид, что привело к собственным правилам сравнения, сложения, вычитания, умножения и деления этих дробей. В принципе, с десятичными дробями можно работать и по правилам обыкновенных дробей. Собственные правила преобразования десятичных дробей упрощают вычисления, а правила преобразования обыкновенных дробей в десятичные, и наоборот, служат связкой между этими видами дроби.

Запись и чтение десятичных дробей позволяет их записывать, сравнивать и производить действия над ними по правилам, очень похожим на правила действий с натуральными числами.

Впервые система десятичных дробей и действий над ними была изложена в XV в. самаркандским математиком и астрономом Джемшид ибн-Масудаль-Каши в книге «Ключ к искусству счета».

Целая часть десятичной дроби отделена от дробной части запятой, в некоторых странах (США) ставят точку. Если в десятичной дроби нет целой части, то перед запятой ставят число 0.

К дробной части десятичной дроби справа можно дописывать любое количество нулей, это величину дроби не изменяет. Дробная часть десятичной дроби читается по последнему значащему разряду.

Например:
0,3 — три десятых
0,75 – семьдесят пять сотых
0,000005 – пять миллионных.

Чтение целой части десятичной дроби такое же, как и натуральных чисел.

Например:
27,5 – двадцать семь. ;
1,57 — одна.

После целой части десятичной дроби произносится слово «целых».

Например:
10.7 — десять целых семь десятых

0,67 – ноль целых шестьдесят семь сотых.

Десятичные знаки – это цифры дробной части. Дробная часть читается не по разрядам (в отличие от натуральных чисел), а целиком, поэтому дробная часть десятичной дроби определяется последним справа значащим разрядом. Разрядная система дробной части десятичной дроби несколько иная, чем у натуральных чисел.

• 1-й разряд после занятой — разряд десятых
• 2-й разряд после запятой — разряд сотых
• 3-й разряд после запятой – разряд тысячных
• 4-й разряд после запятой — разряд десятитысячных
• 5-й разряд после запятой — разряд стотысячных
• 6-й разряд после запятой — разряд миллионных
• 7-й разряд после запятой — разряд десятимиллионных
• 8-й разряд после запятой — разряд стомиллионных

В вычислениях чаще всего используются первые три разряда. Большая разрядность дробной части десятичных дробей используется только в специфических отраслях знаний, где вычисляются бесконечно малые величины.

Перевод десятичной дроби в смешанную дробь состоит н следующем: число, стоящее до запятой записать целой частью смешанной дроби; число, стоящее после запятой – числителем ее дробной части, а в знаменателе дробной части записать единицу со столькими нулями, сколько цифр стоит после запятой.

3.4 Правильный порядок
В предыдущем разделе мы сравнивали числа по их положению на числовой прямой. Это хороший способ сравнивать величины чисел в десятичной записи. Этот способ работает всегда, но это трудоемко и неудобно делать всякий раз, когда нужно сравнить два числа. Существует другой хороший способ выяснить, какое из двух чисел больше.

Рассмотрим числа из предыдущего раздела и сравним 0,05 и 0,2.

Чтобы выяснить, какое число больше, сравним сначала их целые части. Оба числа в нашем примере имеют равное количество целых – 0. Сравним тогда их десятые части. Число 0,05 имеет 0 десятых, а число 0,2 имеет 2 десятых. То, что число 0,05 имеет 5 сотых, ни имеет значения, поскольку десятые доли определяют, что число 0,2 больше. Мы можем, таким образом, записать:

Оба числа имеют 0 целых и 6 десятых, и мы пока не можем определить, какое из них больше. Однако, число 0,612 имеет всего 1 сотую часть, а число 0,62 – две. Тогда, мы можем определить, что

0,62 > 0,612

То, что число 0,612 имеет 2 тысячных, не играет роли, оно все равно меньше, чем 0,62.

Мы можем это проиллюстрировать на картинке:

		0,612
		0,62

Для того, чтобы определить, какое из двух чисел в десятичной записи больше, нужно сделать следующее:

1. Сравнить целые части. То число, у которого целая часть больше и будет больше.

2 . Если целые части равны, сравнить десятые части. То число, у которого десятых частей больше, и будет больше.

3 . Если десятые части равны, сравнить сотые части. То число, у которого сотых частей больше, и будет больше.

4 . Если сотые части равны, сравнить тысячные части. То число, у которого тысячных частей больше, и будет больше.

В этой статье мы рассмотрим тему «сравнение десятичных дробей ». Сначала обсудим общий принцип сравнения десятичных дробей. После этого разберемся, какие десятичные дроби являются равными, а какие – неравными. Дальше научимся определять, какая десятичная дробь больше, а какая меньше. Для этого изучим правила сравнения конечных, бесконечных периодических и бесконечных непериодических дробей. Всю теорию снабдим примерами с подробными решениями. В заключение остановимся на сравнении десятичных дробей с натуральными числами, обыкновенными дробями и смешанными числами.

Сразу скажем, что здесь мы будем говорить лишь о сравнении положительных десятичных дробей (смотрите положительные и отрицательные числа). Остальные случаи разобраны в статьях сравнение рациональных чисел и сравнение действительных чисел .

Общий принцип сравнения десятичных дробей

Исходя из этого принципа сравнения, выводятся правила сравнения десятичных дробей, позволяющие обойтись без перевода сравниваемых десятичных дробей в обыкновенные дроби. Эти правила, а также примеры их применения, мы разберем в следующих пунктах.

По схожему принципу сравниваются конечные десятичные дроби или бесконечные периодические десятичные дроби с натуральными числами , обыкновенными дробями и смешанными числами : сравниваемые числа заменяются соответствующими им обыкновенными дробями, после чего сравниваются обыкновенные дроби.

Что касается сравнения бесконечных непериодических десятичных дробей , то оно обычно сводится к сравнению конечных десятичных дробей. Для этого рассматривается такое количество знаков сравниваемых бесконечных непериодических десятичных дробей, которое позволяет получить результат сравнения.

Равные и неравные десятичные дроби

Сначала введем определения равных и неравных конечных десятичных дробей .

Две конечные десятичные дроби называются равными , если равны соответствующие им обыкновенные дроби, в противном случае эти десятичные дроби называются неравными .

На основании этого определения легко обосновать следующее утверждение: если в конце данной десятичной дроби приписать или отбросить несколько цифр 0 , то получится равная ей десятичная дробь. Например, 0,3=0,30=0,300=… , а 140,000=140,00=140,0=140 .

Действительно, дописывание или отбрасывание в конце десятичной дроби нуля справа соответствует умножению или делению на 10 числителя и знаменателя соответствующей обыкновенной дроби. А мы знаем основное свойство дроби , которое гласит, что умножение или деление числителя и знаменателя дроби на одно и то же натуральное число дает дробь, равную исходной. Этим доказано, что дописывание или отбрасывание нулей справа в дробной части десятичной дроби дает дробь, равную исходной.

Например, десятичной дроби 0,5 отвечает обыкновенная дробь 5/10 , после дописывания нуля справа получается десятичная дробь 0,50 , которой отвечает обыкновенная дробь 50/100 , а . Таким образом, 0,5=0,50 . Обратно, если в десятичной дроби 0,50 отбросить справа 0 , то мы получим дробь 0,5 , так от обыкновенной дроби 50/100 мы придем к дроби 5/10 , но . Следовательно, 0,50=0,5 .

Переходим к определению равных и неравных бесконечных периодических десятичных дробей .

Две бесконечные периодические дроби равны , если равны отвечающие им обыкновенные дроби; если же соответствующие им обыкновенные дроби не равны, то сравниваемые периодические дроби тоже не равны .

Из данного определения следуют три вывода:

• Если записи периодических десятичных дробей полностью совпадают, то такие бесконечные периодические десятичные дроби равны. Например, периодические десятичные дроби 0,34(2987) и 0,34(2987) равны.
• Если периоды сравниваемых десятичных периодических дробей начинаются с одинаковой позиции, первая дробь имеет период 0 , вторая – период 9 , и значение разряда, предшествующего периоду 0 на единицу больше, чем значение разряда, предшествующего периоду 9 , то такие бесконечные периодические десятичные дроби равны. Например, периодические дроби 8,3(0) и 8,2(9) равны, также равны дроби 141,(0) и 140,(9) .
• Две любые другие периодические дроби не являются равными. Приведем примеры неравных бесконечных периодических десятичных дробей: 9,0(4) и 7,(21) , 0,(12) и 0,(121) , 10,(0) и 9,8(9) .

Осталось разобраться с равными и неравными бесконечными непериодическими десятичными дробями . Как известно, такие десятичные дроби не могут быть переведены в обыкновенные дроби (такие десятичные дроби представляют иррациональные числа), поэтому сравнение бесконечных непериодических десятичных дробей нельзя свести к сравнению обыкновенных дробей.

Две бесконечные непериодические десятичные дроби равны , если их записи полностью совпадают.

Но есть один нюанс: невозможно увидеть «законченную» запись бесконечных непериодических десятичных дробей, следовательно, невозможно убедиться и в полном совпадении их записей. Как же быть?

При сравнении бесконечных непериодических десятичных дробей рассматривают лишь конечное число знаков сравниваемых дробей, которое позволяет сделать необходимые выводы. Таким образом, сравнение бесконечных непериодических десятичных дробей сводится к сравнению конечных десятичных дробей.

При таком подходе можно говорить о равенстве бесконечных непериодических десятичных дробей лишь с точностью до рассматриваемого разряда. Приведем примеры. Бесконечные непериодические десятичные дроби 5,45839… и 5,45839… равны с точностью до стотысячных, так как равны конечные десятичные дроби 5,45839 и 5,45839 ; непериодические десятичные дроби 19,54… и 19,54810375… равны с точностью до сотых, так как равны дроби 19,54 и 19,54 .

Неравенство бесконечных непериодических десятичных дробей при таком подходе устанавливается вполне определенно. Например, бесконечные непериодические десятичные дроби 5,6789… и 5,67732… не равны, так как очевидны различия в их записях (не равны конечные десятичные дроби 5,6789 и 5,6773 ). Бесконечные десятичные дроби 6,49354… и 7,53789… тоже не равны.

Правила сравнения десятичных дробей, примеры, решения

После установления факта неравенства двух десятичных дробей, часто нужно узнать, какая из этих дробей больше, а какая – меньше другой. Сейчас мы разберем правила сравнения десятичных дробей, позволяющие ответить на поставленный вопрос.

Во многих случаях бывает достаточно сравнить целые части сравниваемых десятичных дробей. Справедливо следующее правило сравнения десятичных дробей : больше та десятичная дробь, целая часть которой больше, и меньше та десятичная дробь, целая часть которой меньше.

Это правило относится как к конечным десятичным дробям, так и к бесконечным. Рассмотрим решения примеров.

Сравните десятичные дроби 9,43 и 7,983023… .

Очевидно, данные десятичные дроби не равны. Целая часть конечной десятичной дроби 9,43 равна 9 , а целая часть бесконечной непериодической дроби 7,983023… равна 7 . Так как 9>7 (смотрите сравнение натуральных чисел), то 9,43>7,983023 .

Какая из десятичных дробей 49,43(14) и 1 045,45029… меньше?

Целая часть периодической дроби 49,43(14) меньше, чем целая часть бесконечной непериодической десятичной дроби 1 045,45029… , следовательно, 49,43(14) 5 ). Следовательно, 0,87>0,8521 .

Иногда, чтобы выполнить сравнение конечных десятичных дробей с разным количеством десятичных знаков, к дроби с меньшим количеством десятичных знаков приходится дописывать некоторое количество нулей справа. Достаточно удобно уравнивать количество десятичных знаков до начала сравнения конечных десятичных дробей, дописав к одной из них некоторое количество нулей справа.

Сравните конечные десятичные дроби 18,00405 и 18,0040532 .

Очевидно, данные дроби неравны, так как их записи отличаются, но при этом они имеют равные целые части (18=18 ).

Перед поразрядным сравнением дробных частей данных дробей уравняем количество десятичных знаков. Для этого припишем две цифры 0 в конце дроби 18,00405 , при этом получим равную ей десятичную дробь 18,0040500 .

Значения десятичных разрядов дробей 18,0040500 и 18,0040532 равны вплоть до стотысячных, а значение разряда миллионных дроби 18,0040500 меньше значения соответствующего разряда дроби 18,0040532 (0

Источник статьи: http://ik-ptz.ru/russian-language/chto-bolshe-desyatye-ili-sotye-doli-chtenie-desyatichnyh-drobei-sravnenie.html

Десятичные дроби – для чайников

Действия с десятичными дробями – деление умножение, сложение, вычитание, сравнение. Разбор примеров.

Между прочим, большинство ошибок на экзаменах происходят как раз из-за незнания простейших действий вроде этих.

Так что читай эту статью и отрабатывай скиллы.

Десятичные дроби – коротко о главном

1. Определение

Десятичной дробью называется обыкновенная дробь, знаменателем которой является \( 10\) в какой-либо степени.

2. Конечная и бесконечная десятичная дробь

Десятичная дробь может быть:

• конечной, если она содержит конечное число цифр после запятой (\( \displaystyle \frac<8><10>,\ \frac<13><100>,\frac<49><1000>\));
• бесконечной, в том числе периодичной, если конечное число цифр определить не определено (\( 0,05882352941…\));
• периодической, если её последовательность цифр после запятой, начиная с некоторого места, представляет собой периодически повторяющуюся группу цифр (\( \displaystyle \frac<1><7>=0,\underbrace<142857>_<<период>>\underbrace<142857>_<период>142…=0,\left( 142857 \right)\))

3. Свойства десятичных дробей

• Десятичная дробь не меняется, если справа добавить нули \( \displaystyle \frac<3><100>=0,03=0,030=0,030000\)и т.д.;
• Десятичная дробь не меняется, если удалить нули, расположенные в конце десятичной дроби: \( 0,014330000=0,01433\);
• Десятичная дробь возрастает в \( 10\), \( 100\), \( 1000\) и т.д. раз, если перенести десятичную точку на одну, две, три и т.д. позиций вправо: \( 0,0125\cdot 100=1,25\) (перенесли запятую на \( 2\) знака вправо – умножили на \( 100\) и дробь возросла в \( 100\) раз);
• Десятичная дробь уменьшается в \( 10\), \( 100\), \( 1000\) и т.д. раз, если перенести десятичную точку на одну, две, три и т.д. позиций влево: \( 124,56:100=1,2456\) (перенесли запятую на \( 2\) знака влево – разделили на \( 100\) и дробь уменьшилась в \( 100\) раз).

4. Сложение десятичных дробей

Сложение происходит, как и сложение натуральных чисел в столбик, при этом запятая в ответе ставиться четко на том же месте, как и в складываемых числах.

5. Вычитание десятичных дробей

Так же, как и при сложении, при вычитании десятичные дроби записываются «столбиком»:

6. Умножение десятичных дробей

Десятичные дроби также записываются в столбик и умножаются как обыкновенные числа. При умножении нам неважно, стоят ли запятые под запятыми и так далее.

Однако, удобно, когда числа выровнены по правому краю – умножение происходит более упорядочено.

7. Деление десятичных дробей

Деление десятичной дроби на натуральное число

• Делим десятичную дробь на натуральное число по правилам деления в столбик, не обращая внимания на запятую в делимом (то число, которое мы делим на какое-либо другое число)
• Ставим в частном запятую, когда заканчивается деление целой части делимого.

Деление десятичных дробей друг на друга

• Считаем количество знаков справа от запятой в десятичной дроби.
• Умножаем и делимое, и делитель на 10, 100 или 1000 и т.д., в зависимости от того, сколько мы насчитали знаков в первом пункте. Умножать необходимо, чтобы превратить десятичную дробь в целое число.

Десятичные дроби – подробнее

Конечно, ты знаешь, что такое обыкновенная дробь. Например, \( \displaystyle \frac<1><3>,\ \frac<1><4>,\frac<5><112>\).

Наравне с приведенными выше дробями существуют дроби \( \displaystyle \frac<8><10>,\ \frac<13><100>,\frac<49><1000>\) и т.д.

Такие дроби можно записать намного удобнее и более кратко, то есть:

Данного вида дроби называются десятичными. Иными словами:

Десятичной дробью называется обыкновенная дробь, знаменателем которой является \( 10\) в какой-либо степени (первый пример – \( 10\) в первой степени, второй – \( 10\) во второй степени и т.д.).

Ты наверняка знаешь, что каждая цифра после запятой имеет свое название. На всякий случай напомню тебе про них, чтобы в дальнейшем мы говорили на одном языке:

Это огромное число читается по следующему алгоритму:

1. Сначала читается число, стоящее до запятой и добавляется слово «целых»: ««\( 46\) целых»;
2. Затем читается как обыкновенное число слева после запятой и добавляется слово, обозначающее название самой последней цифры. В нашем случае – «одна тысяча двести тридцать четыре десятитысячные».

А теперь прочитаем все вместе – «\( 46\) целых одна тысяча двести тридцать четыре десятитысячные». Разобрался? Переходим к визуализации полученных знаний!

Итак, небольшая тренировка на понимание, что такое эта десятичная дробь! Нарисуй квадрат \( 10\) на \( 10\) и закрась какую-нибудь его часть равную:

Справился? Проверяем, что у тебя получилось.

Во-первых, квадрат \( 10\) на \( 10\) состоит из \( 100\) клеточек. Соответственно, \( 0.05\) – \( 5\) клеточек из \( 100\); \( 0,4\) – \( 40\) клеточек из \( 100\) и так далее.

Наверняка, наибольшее затруднение составило последнее число – \( -0,245\). На картинке это необходимо отразить как 24,5 клетки.

С понятиями разобрались, теперь научимся переводить из десятичной дроби в обыкновенную и обратно.

Перевод из десятичной дроби в обыкновенную и обратно

Уверена, что ты с легкостью справился! А как насчет обратного перевода? Из обыкновенных в десятичные?

Попробуй свои силы на вот этих дробях:

Если ты со всем справился, можешь пропускать следующий абзац, а если где-то допустил ошибку, внимательно прочти о том, как легко и 100% правильно переводить дроби из обыкновенных в десятичные.

1. Смотрим на дробь и определяем, есть ли у нее целая часть? Если есть, выделяем целую часть, записываем ее, и ставим запятую.
2. После запятой должно быть столько знаков, сколько нулей стоит в знаменателе. Например, дробь \( \displaystyle \frac<4><1000>\) – \( 3\) нуля в знаменателе, соответственно, мы как бы мысленно выделяем \( 3\) ячейки.
3. Затем записываем числитель – \( 4\), но выравниваем его по правому краю, а в пустые ячейки вставляем нули.

Разобрался? Посмотри еще раз эту маленькую «инструкцию»:

Я думаю, ты во всем-всем разобрался! Потренируемся? Попробуй поработать еще с вот этими дробями:

Виды десятичных дробей

Десятичная дробь может быть:

• конечной, если она содержит конечное число цифр после запятой (\( \displaystyle \frac<8><10>,\ \frac<13><100>,\frac<49><1000>\));
• бесконечной, в том числе периодичной, если конечное число цифр определить не определено (\( 0,05882352941…\));
• периодической, если её последовательность цифр после запятой, начиная с некоторого места, представляет собой периодически повторяющуюся группу цифр (\( \displaystyle \frac<1><7>=0,\underbrace<142857>_<<период>>\underbrace<142857>_<период>142…=0,\left( 142857 \right)\)).

Поговорим сначала о конечных дробях.

Конечная десятичная дробь

Само собой понятно, что дроби \( \displaystyle \frac<8><10>,\ \frac<13><100>,\frac<49><1000>\) являются конечными, ведь знаменатель дроби уже представлен как единица с последующими нулями, и поэтому мы сразу можем сказать, что данную обыкновенную дробь можно перевести в конечную десятичную. А что ты скажешь насчет этой дроби: \( \displaystyle \frac<1><4>\)? Ее знаменатель далеко не единица с последующими нулями, но ты четко знаешь, что у нее есть десятичный «аналог»:

То есть, чтобы определить, можно ли перевести дробь в десятичную, необходимо умножить числитель и знаменатель на одно и то же число, такое, чтобы знаменатель стал равен \( 10\), \( 100\), \( 1000\) и так далее.

Усвоил? Постарайся представить в виде конечной десятичной дроби следующие обыкновенные дроби:

Справился? Молодец. Выходим на новый уровень и переходим к бесконечным десятичным дробям.

Бесконечная десятичная дробь

Итак, бери калькулятор и дели \( 1\) на \( 17\). Поделил? Ты получил \( 0,05882352941\) и дальше окошко калькулятора не показывает… Это тоже является десятичной дробью, только данная десятичная дробь является бесконечной. Ты сейчас скажешь, а как же наше определение?

Десятичной дробью называется обыкновенная дробь, знаменателем которой является \( 10\) в какой-либо степени (первый пример – \( 10\) в первой степени, второй – \( 10\) во второй степени и т.д.).

Все очень просто и никаких противоречий с определением нет. В данном случае нам необходимо привести наш знаменатель к \( <<10>^>\), с учетом, что \( n\) это какое-либо бесконечное число, которое мы не можем «обозреть» взглядом», или иными словами – \( n\to +\infty \)

Бесконечной десятичной дробью называется обыкновенная дробь, в записи которой после запятой содержится бесконечное количество цифр.

Как правило, в задачах, где встречаются бесконечные десятичные дроби, просят указать ответ либо с округлением (например, до десятых, или до сотых), либо записать в виде обыкновенной дроби, то есть как \( \displaystyle \frac<1><17>\).

Подумай, какой самый популярный пример можно привести на тему «бесконечная десятичная дробь»? Правильно! Число \( \pi \) является бесконечной десятичной дробью. Во всем мире люди договорились, что для решения математических задач принято, что \( \pi =3,14\), но это далеко не так. Число \( \pi \) не имеет определенного завершения. Оно настолько бесконечно, что ежегодно в мире проводятся соревнования по запоминанию числа \( \pi \). Мировой рекорд по запоминанию знаков числа \( \pi \) после запятой принадлежит китайцу Лю Чао, который в 2006 году в течение 24 часов и 4 минут воспроизвёл 67 890 знаков после запятой без ошибки! Все 67 890 знаков после запятой мы приводить не будем, а приведем несколько сокращенную запись:

Думаю, этого хватит, чтобы оценить «масштабы» данного числа.

Наравне с бесконечными десятичными дробями существуют периодические десятичные дроби. Они так же не имеют конца, но последующие числа в них повторяются, например, попробуй перевести в десятичную дробь \( \displaystyle \frac<1><3>\). Что у тебя получилось?

Чтобы не повторять число \( 3\) много много раз, решили говорить «ноль целых и три в периоде», так как тройка будет повторяться после запятой бесконечное число раз. Из этого умозаключения следует определение:

Дробь называется периодической, если её последовательность цифр после запятой, начиная с некоторого места, представляет собой периодически повторяющуюся группу цифр.

Чтобы кратко записать такую дробь, период (повторяющиеся цифры после запятой) пишут в скобках:

\( \displaystyle \frac<1><3>=0,\underbrace<3>_<период>33333333….=0,\left( 3 \right)\)

\( \displaystyle \frac<1><7>=0,\underbrace<142857>_<<период>>\underbrace<142857>_<период>142…=0,\left( 142857 \right)\)

Важно, что период не может начинаться слева от запятой:

\( \displaystyle \frac<100><7>=\underbrace<14,2857>_<не период>1428571428571…=14,\left( 285714 \right)\).

Источник статьи: http://youclever.org/book/desyatichnye-drobi-1/

Напишите цифрами десятичную дробь : одна целая три сотых, одна целая три тысячных?

Русский язык | 10 – 11 классы

Напишите цифрами десятичную дробь : одна целая три сотых, одна целая три тысячных.

Нуль целых одиннадцать сотых, одна целая пять сотых, десять целых восемь сотых.

Пять целых сорок семь тысячных, сорок целых сто пять тысячных, двадцать целых две тысячные.

Нуль целых сто тридцать семь десятитысячных, десять целых пятнадцать стотысячных.

1, 031, 0030, 111, 0510, 085, 04740, 10520, 0020, 013710, 00015.

1, 03 ; 1, 003, 0, 11 ; 1, 05 ; 10, 08.

5, 048 ; 40, 105 ; 20, 002 ; 0, 0137 ; 10, 00015.

Просклонять пятьсот десять целых семьдесят три сотых?

Просклонять пятьсот десять целых семьдесят три сотых.

Проверте написание числа прописью 0?

Проверте написание числа прописью 0.

0021 Ноль целых ноль тысячных ноль сотых двадцать один?

Просклоняйте по падежам : одиннадцать целых тридцать пять сотых, тринадцать целых сорок семь сотых?

Просклоняйте по падежам : одиннадцать целых тридцать пять сотых, тринадцать целых сорок семь сотых.

Помогите пожалуйста, осталось только это.

К семнадцать целых девяносто девять сто пятьдесят шестых прибавить шестнадцать восемнадцатых?

К семнадцать целых девяносто девять сто пятьдесят шестых прибавить шестнадцать восемнадцатых.

К ста сорока четырем целых двадцать три шестьдесят седьмым прибавить пятнадцать третих.

Ноль целых шестьдесят три сотых прибавить тринадцать тринадцатых.

Пожалуйста напишете правильно.

Запишите кооичественные числительные, распределяя их на три группы : а) числительные, обозначающие целые числа ; б) дробные числительные ; в) собирательные числительные?

Запишите кооичественные числительные, распределяя их на три группы : а) числительные, обозначающие целые числа ; б) дробные числительные ; в) собирательные числительные.

Дополните каждую группу тремя примерами.

Два, пятьдесят, пятеро, одна восьмая, пять целых одна десятая, двести, одиннадцать, трое, три четвёртых, шестеро, двадцать пять, оба, одна целая девять сотых, восемь миллионов.

Написать число прописью 0?

Написать число прописью 0.

Ноль целых ноль тысячных ноль сотых двадцать один?

Проверте правильно ли написала, спасибо.

Правильно прочитайте и запишите одна третья пять седьмых двадцать семь целых шесть десятых одна целая восемь десятых?

Правильно прочитайте и запишите одна третья пять седьмых двадцать семь целых шесть десятых одна целая восемь десятых.

Как правильно написать, 30, 7 , тридцать целых семь десятых или семь сотых ?

Как правильно написать, 30, 7 , тридцать целых семь десятых или семь сотых ?

Просклонять по падежам числительные две целых одна третья, десять целых три седьмых, одиннадцать целых пятнадцать сороковых?

Просклонять по падежам числительные две целых одна третья, десять целых три седьмых, одиннадцать целых пятнадцать сороковых.

Как правильно пишется – шестисот целых и двадцать сотых?

Как правильно пишется – шестисот целых и двадцать сотых?

На этой странице сайта размещен вопрос Напишите цифрами десятичную дробь : одна целая три сотых, одна целая три тысячных? из категории Русский язык с правильным ответом на него. Уровень сложности вопроса соответствует знаниям учеников 10 – 11 классов. Здесь же находятся ответы по заданному поиску, которые вы найдете с помощью автоматической системы. Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по заданной теме. На этой странице можно обсудить все варианты ответов с другими пользователями сайта и получить от них наиболее полную подсказку.

Набережная существительное одной чертой(какая) красивая двумя чертами Около подчеркиваем волнистой линией в. В сл моря одна черта существительное Время дня одной чертой сущ какое жаркое двумя чертами ветвями какими большими.

А) парочку Б) дразнится В) стишок.

1 схема. Солнце светит. Повествовательное. 2 схема. Девочка делает зарядку. Повествовательное. 3 схема. С дерева упало сочное яблоко. Повествовательное. 4схема. Мальчик думает о маме и о папе. Повествовательное. 5схема. Крпсивый лебедь п..

Жила – была бедная старушка. Такая она была бедная, что порой ей даже не из чего было хлеба испечь. И была у неё соседка – злыдня, которая эту старушку непрестанно бедностью её попрекала. И вдруг заметила соседка : как только она принимается хлеб ..

1. Звуки речи 2. Сами звуки 1. Песня 2. Басня 3. Конец.

Розы – существительное , укрывают – глагол , на – предлог, зиму – существительное , потому – наречие , что – наречие , побеги – существительное , непокрытая – прилагательное , снегом – существительное , обмерзают – глагол , при – предлог , низких – п..

Начнем с главных членов предложения. 1) Хорош лес 2) окрашена листва 3) расстилаются листья 4) видны шляпки а теперь определение и дополнение. Дополнение(сущ. ) – 1) дни, 2) цвет, 3) – , 4) – . Определение(в данном случае это прилагательные) – 1)..

ПрЕломление ПрЕподнести ПрЕкратить споры ПрЕстиж ПрЕзумция ПрЕмьера ПрЕвратно понятый ПрЕсимпатичный ПрЕсимпатичный.

Решение в приложении Всё остальное у Вас правильно.

Раз – вед – чи – ки | р а с в * э ч * и к * и | 4 слога р (р) согл. , зв. Непарн. , тв. Непарн. , а (а) глас. , безуд. , з (с) согл. , глух. Парн. , тв. Парн. , в (в) согл. , зв. Парн. , мягк. Парн. , е (э) глас. , уд. , д ч(ч) сог..

Источник статьи: http://russkij-azyk.my-dict.ru/q/428371_napisite-ciframi-desaticnuu-drob-odna-celaa/

Портал для школьника. Самоподготовка

Что больше десятые или сотые доли. Чтение десятичных дробей

Десятичная дробь в обязательном порядке содержит запятую. Та числовая часть дроби, которая располагается левее запятой, называется целой; правее – дробной:

5,28 5 – целая часть 28 – дробная часть

Дробная часть десятичной дроби состоит из десятичных знаков (десятичных разрядов):

• десятые – 0,1 (одна десятая);
• сотые – 0,01 (одна сотая);
• тысячные – 0,001 (одна тысячная);
• десятитысячные – 0,0001 (одна десятитысячная);
• стотысячные – 0,00001 (одна стотысячная);
• миллионные – 0,000001 (одна миллионная);
• десятимиллионные – 0,0000001 (одна десятимиллионная);
• стомиллионные – 0,00000001 (одна стомиллионная);
• миллиардные – 0,000000001 (одна миллиардная) и т. д.

• прочитать число, составляющее целую часть дроби и добавить слово “целых “;
• прочитать число, составляющее дробную часть дроби и добавить название младшего разряда.

• 0,25 – ноль целых двадцать пять сотых;
• 9,1 – девять целых одна десятая;
• 18,013 – восемнадцать целых тринадцать тысячных;
• 100,2834 – сто целых две тысячи восемьсот тридцать четыре десятитысячных.

Запись десятичных дробей

Чтобы записать десятичную дробь, необходимо:

• записать целую часть дроби и поставить запятую (число, означающее целую часть дроби всегда заканчивается словом “целых “);
• записать дробную часть дроби таким образом, чтобы последняя цифра попала в нужный разряд (при отсутствии значащих цифр в определенных десятичных разрядах они заменяются нулями).

• двадцать целых девять десятых – 20,9 – в этом примере все просто;
• пять целых одна сотая – 5,01 – слово “сотая” означает, что после запятой должны стоять две цифры, но, поскольку в числе 1 нет разряда десятых, он заменяется нулем;
• ноль целых восемьсот восемь тысячных – 0,808;
• три целых пятнадцать десятых – такую десятичную дробь записать невозможно, потому, что в произношении дробной части допущена ошибка – число 15 содержит два разряда, а слово “десятых” подразумевает только один. Правильно будет три целых пятнадцать сотых (или тысячных, десятитысячных и т. д.).

Сравнение десятичных дробей

Сравнение десятичных дробей проводится аналогично сравнению натуральных чисел .

1. сначала сравниваются целые части дробей – больше будет та десятичная дробь у которой больше ее целая часть;
2. если целые части дробей равны, сравнивают поразрядно дробные части, слева направо, начиная от запятой: десятые, сотые, тысячные и т.д. Сравнение ведут до первого несовпадения – больше будет та десятичная дробь у которой будет больше неравная цифра в соответствующем разряде дробной части. Например: 1,28 3 > 1,27 9, т. к. в сотых разрядах у первой дроби стоит 8, а у второй 7.

Десятичная дробь отличается от обыкновенной дроби тем, что знаменатель у нее — это разрядная единица.

Десятичные дроби выделены из обыкновенных дробей в отдельный вид, что привело к собственным правилам сравнения, сложения, вычитания, умножения и деления этих дробей. В принципе, с десятичными дробями можно работать и по правилам обыкновенных дробей. Собственные правила преобразования десятичных дробей упрощают вычисления, а правила преобразования обыкновенных дробей в десятичные, и наоборот, служат связкой между этими видами дроби.

Запись и чтение десятичных дробей позволяет их записывать, сравнивать и производить действия над ними по правилам, очень похожим на правила действий с натуральными числами.

Впервые система десятичных дробей и действий над ними была изложена в XV в. самаркандским математиком и астрономом Джемшид ибн-Масудаль-Каши в книге «Ключ к искусству счета».

Целая часть десятичной дроби отделена от дробной части запятой, в некоторых странах (США) ставят точку. Если в десятичной дроби нет целой части, то перед запятой ставят число 0.

К дробной части десятичной дроби справа можно дописывать любое количество нулей, это величину дроби не изменяет. Дробная часть десятичной дроби читается по последнему значащему разряду.

Например:
0,3 — три десятых
0,75 – семьдесят пять сотых
0,000005 – пять миллионных.

Чтение целой части десятичной дроби такое же, как и натуральных чисел.

Например:
27,5 – двадцать семь. ;
1,57 — одна.

После целой части десятичной дроби произносится слово «целых».

Например:
10.7 — десять целых семь десятых

0,67 – ноль целых шестьдесят семь сотых.

Десятичные знаки – это цифры дробной части. Дробная часть читается не по разрядам (в отличие от натуральных чисел), а целиком, поэтому дробная часть десятичной дроби определяется последним справа значащим разрядом. Разрядная система дробной части десятичной дроби несколько иная, чем у натуральных чисел.

• 1-й разряд после занятой — разряд десятых
• 2-й разряд после запятой — разряд сотых
• 3-й разряд после запятой – разряд тысячных
• 4-й разряд после запятой — разряд десятитысячных
• 5-й разряд после запятой — разряд стотысячных
• 6-й разряд после запятой — разряд миллионных
• 7-й разряд после запятой — разряд десятимиллионных
• 8-й разряд после запятой — разряд стомиллионных

В вычислениях чаще всего используются первые три разряда. Большая разрядность дробной части десятичных дробей используется только в специфических отраслях знаний, где вычисляются бесконечно малые величины.

Перевод десятичной дроби в смешанную дробь состоит н следующем: число, стоящее до запятой записать целой частью смешанной дроби; число, стоящее после запятой – числителем ее дробной части, а в знаменателе дробной части записать единицу со столькими нулями, сколько цифр стоит после запятой.

3.4 Правильный порядок
В предыдущем разделе мы сравнивали числа по их положению на числовой прямой. Это хороший способ сравнивать величины чисел в десятичной записи. Этот способ работает всегда, но это трудоемко и неудобно делать всякий раз, когда нужно сравнить два числа. Существует другой хороший способ выяснить, какое из двух чисел больше.

Рассмотрим числа из предыдущего раздела и сравним 0,05 и 0,2.

Чтобы выяснить, какое число больше, сравним сначала их целые части. Оба числа в нашем примере имеют равное количество целых – 0. Сравним тогда их десятые части. Число 0,05 имеет 0 десятых, а число 0,2 имеет 2 десятых. То, что число 0,05 имеет 5 сотых, ни имеет значения, поскольку десятые доли определяют, что число 0,2 больше. Мы можем, таким образом, записать:

Оба числа имеют 0 целых и 6 десятых, и мы пока не можем определить, какое из них больше. Однако, число 0,612 имеет всего 1 сотую часть, а число 0,62 – две. Тогда, мы можем определить, что

0,62 > 0,612

То, что число 0,612 имеет 2 тысячных, не играет роли, оно все равно меньше, чем 0,62.

Мы можем это проиллюстрировать на картинке:

		0,612
		0,62

Для того, чтобы определить, какое из двух чисел в десятичной записи больше, нужно сделать следующее:

1. Сравнить целые части. То число, у которого целая часть больше и будет больше.

2 . Если целые части равны, сравнить десятые части. То число, у которого десятых частей больше, и будет больше.

3 . Если десятые части равны, сравнить сотые части. То число, у которого сотых частей больше, и будет больше.

4 . Если сотые части равны, сравнить тысячные части. То число, у которого тысячных частей больше, и будет больше.

В этой статье мы рассмотрим тему «сравнение десятичных дробей ». Сначала обсудим общий принцип сравнения десятичных дробей. После этого разберемся, какие десятичные дроби являются равными, а какие – неравными. Дальше научимся определять, какая десятичная дробь больше, а какая меньше. Для этого изучим правила сравнения конечных, бесконечных периодических и бесконечных непериодических дробей. Всю теорию снабдим примерами с подробными решениями. В заключение остановимся на сравнении десятичных дробей с натуральными числами, обыкновенными дробями и смешанными числами.

Сразу скажем, что здесь мы будем говорить лишь о сравнении положительных десятичных дробей (смотрите положительные и отрицательные числа). Остальные случаи разобраны в статьях сравнение рациональных чисел и сравнение действительных чисел .

Общий принцип сравнения десятичных дробей

Исходя из этого принципа сравнения, выводятся правила сравнения десятичных дробей, позволяющие обойтись без перевода сравниваемых десятичных дробей в обыкновенные дроби. Эти правила, а также примеры их применения, мы разберем в следующих пунктах.

По схожему принципу сравниваются конечные десятичные дроби или бесконечные периодические десятичные дроби с натуральными числами , обыкновенными дробями и смешанными числами : сравниваемые числа заменяются соответствующими им обыкновенными дробями, после чего сравниваются обыкновенные дроби.

Что касается сравнения бесконечных непериодических десятичных дробей , то оно обычно сводится к сравнению конечных десятичных дробей. Для этого рассматривается такое количество знаков сравниваемых бесконечных непериодических десятичных дробей, которое позволяет получить результат сравнения.

Равные и неравные десятичные дроби

Сначала введем определения равных и неравных конечных десятичных дробей .

Две конечные десятичные дроби называются равными , если равны соответствующие им обыкновенные дроби, в противном случае эти десятичные дроби называются неравными .

На основании этого определения легко обосновать следующее утверждение: если в конце данной десятичной дроби приписать или отбросить несколько цифр 0 , то получится равная ей десятичная дробь. Например, 0,3=0,30=0,300=… , а 140,000=140,00=140,0=140 .

Действительно, дописывание или отбрасывание в конце десятичной дроби нуля справа соответствует умножению или делению на 10 числителя и знаменателя соответствующей обыкновенной дроби. А мы знаем основное свойство дроби , которое гласит, что умножение или деление числителя и знаменателя дроби на одно и то же натуральное число дает дробь, равную исходной. Этим доказано, что дописывание или отбрасывание нулей справа в дробной части десятичной дроби дает дробь, равную исходной.

Например, десятичной дроби 0,5 отвечает обыкновенная дробь 5/10 , после дописывания нуля справа получается десятичная дробь 0,50 , которой отвечает обыкновенная дробь 50/100 , а . Таким образом, 0,5=0,50 . Обратно, если в десятичной дроби 0,50 отбросить справа 0 , то мы получим дробь 0,5 , так от обыкновенной дроби 50/100 мы придем к дроби 5/10 , но . Следовательно, 0,50=0,5 .

Переходим к определению равных и неравных бесконечных периодических десятичных дробей .

Две бесконечные периодические дроби равны , если равны отвечающие им обыкновенные дроби; если же соответствующие им обыкновенные дроби не равны, то сравниваемые периодические дроби тоже не равны .

Из данного определения следуют три вывода:

• Если записи периодических десятичных дробей полностью совпадают, то такие бесконечные периодические десятичные дроби равны. Например, периодические десятичные дроби 0,34(2987) и 0,34(2987) равны.
• Если периоды сравниваемых десятичных периодических дробей начинаются с одинаковой позиции, первая дробь имеет период 0 , вторая – период 9 , и значение разряда, предшествующего периоду 0 на единицу больше, чем значение разряда, предшествующего периоду 9 , то такие бесконечные периодические десятичные дроби равны. Например, периодические дроби 8,3(0) и 8,2(9) равны, также равны дроби 141,(0) и 140,(9) .
• Две любые другие периодические дроби не являются равными. Приведем примеры неравных бесконечных периодических десятичных дробей: 9,0(4) и 7,(21) , 0,(12) и 0,(121) , 10,(0) и 9,8(9) .

Осталось разобраться с равными и неравными бесконечными непериодическими десятичными дробями . Как известно, такие десятичные дроби не могут быть переведены в обыкновенные дроби (такие десятичные дроби представляют иррациональные числа), поэтому сравнение бесконечных непериодических десятичных дробей нельзя свести к сравнению обыкновенных дробей.

Две бесконечные непериодические десятичные дроби равны , если их записи полностью совпадают.

Но есть один нюанс: невозможно увидеть «законченную» запись бесконечных непериодических десятичных дробей, следовательно, невозможно убедиться и в полном совпадении их записей. Как же быть?

При сравнении бесконечных непериодических десятичных дробей рассматривают лишь конечное число знаков сравниваемых дробей, которое позволяет сделать необходимые выводы. Таким образом, сравнение бесконечных непериодических десятичных дробей сводится к сравнению конечных десятичных дробей.

При таком подходе можно говорить о равенстве бесконечных непериодических десятичных дробей лишь с точностью до рассматриваемого разряда. Приведем примеры. Бесконечные непериодические десятичные дроби 5,45839… и 5,45839… равны с точностью до стотысячных, так как равны конечные десятичные дроби 5,45839 и 5,45839 ; непериодические десятичные дроби 19,54… и 19,54810375… равны с точностью до сотых, так как равны дроби 19,54 и 19,54 .

Неравенство бесконечных непериодических десятичных дробей при таком подходе устанавливается вполне определенно. Например, бесконечные непериодические десятичные дроби 5,6789… и 5,67732… не равны, так как очевидны различия в их записях (не равны конечные десятичные дроби 5,6789 и 5,6773 ). Бесконечные десятичные дроби 6,49354… и 7,53789… тоже не равны.

Правила сравнения десятичных дробей, примеры, решения

После установления факта неравенства двух десятичных дробей, часто нужно узнать, какая из этих дробей больше, а какая – меньше другой. Сейчас мы разберем правила сравнения десятичных дробей, позволяющие ответить на поставленный вопрос.

Во многих случаях бывает достаточно сравнить целые части сравниваемых десятичных дробей. Справедливо следующее правило сравнения десятичных дробей : больше та десятичная дробь, целая часть которой больше, и меньше та десятичная дробь, целая часть которой меньше.

Это правило относится как к конечным десятичным дробям, так и к бесконечным. Рассмотрим решения примеров.

Сравните десятичные дроби 9,43 и 7,983023… .

Очевидно, данные десятичные дроби не равны. Целая часть конечной десятичной дроби 9,43 равна 9 , а целая часть бесконечной непериодической дроби 7,983023… равна 7 . Так как 9>7 (смотрите сравнение натуральных чисел), то 9,43>7,983023 .

Какая из десятичных дробей 49,43(14) и 1 045,45029… меньше?

Целая часть периодической дроби 49,43(14) меньше, чем целая часть бесконечной непериодической десятичной дроби 1 045,45029… , следовательно, 49,43(14) 5 ). Следовательно, 0,87>0,8521 .

Иногда, чтобы выполнить сравнение конечных десятичных дробей с разным количеством десятичных знаков, к дроби с меньшим количеством десятичных знаков приходится дописывать некоторое количество нулей справа. Достаточно удобно уравнивать количество десятичных знаков до начала сравнения конечных десятичных дробей, дописав к одной из них некоторое количество нулей справа.

Сравните конечные десятичные дроби 18,00405 и 18,0040532 .

Очевидно, данные дроби неравны, так как их записи отличаются, но при этом они имеют равные целые части (18=18 ).

Перед поразрядным сравнением дробных частей данных дробей уравняем количество десятичных знаков. Для этого припишем две цифры 0 в конце дроби 18,00405 , при этом получим равную ей десятичную дробь 18,0040500 .

Значения десятичных разрядов дробей 18,0040500 и 18,0040532 равны вплоть до стотысячных, а значение разряда миллионных дроби 18,0040500 меньше значения соответствующего разряда дроби 18,0040532 (0

Источник статьи: http://ik-ptz.ru/russian-language/chto-bolshe-desyatye-ili-sotye-doli-chtenie-desyatichnyh-drobei-sravnenie.html

Десятичные дроби | теория по математике 🎲 числа и вычисления

Десятичная дробь — дробь, которая представляет собой способ представление числа в виде записи числа с запятой, где цифры перед запятой называются целой частью, а цифры после запятой – дробной частью (десятичной частью).

Десятичные дроби получают из записи обыкновенных дробей со знаменателем 10, 100, 1000 и так далее. Например, десятичные дроби:

4,56 – четыре целых пятьдесят шесть сотых 18,234 – восемнадцать целых двести тридцать четыре тысячных 78,6 – семьдесят восемь целых шесть десятых

Чтение десятичной части (десятых, сотых и так далее) зависит от количества цифр после запятой. Если цифра одна, то читают – десятых (в числе десять – один нуль, это соответствует одной цифре). Если две цифры после запятой, то читают – сотых (в сотне два нуля).

Десятичные дроби получаются из обыкновенных дробей: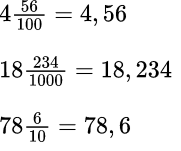

Сложение (вычитание) десятичных дробей

1. Записать их друг под другом так, чтобы при записи запятая оказалась под запятой и соответствующий разряд под соответствующим.
2. Уравнять количество знаков после запятой, добавляя недостающие нулями.
3. Выполнить сложение (вычитание) в столбик, не обращая внимания на запятую.
4. Поставить запятую под запятыми.

Если складывают (вычитают) целое число и десятичную дробь, то нужно поставить запятую после целого числа и приписать необходимое количество нулей после запятой.

Пример №1. Запись, где запятая под запятой и соответствующий разряд под соответствующим.

Пример №2. Запись, где также запятая под запятой, а во втором числе дописан нуль, чтобы уравнять количество знаков после запятой.

Пример №3. В первом слагаемом нет десятичной части, поэтому, после числа 56 поставили запятую и добавили нужное количество нулей.

Умножение десятичных дробей

При умножении двух десятичных дробей в столбик необходимо:

1. Написать числа одно под другим, не обращая внимания на запятую
2. Выполнить умножение в столбик
3. В ответе отделить столько цифр справа запятой, сколько их в обоих множителях вместе. Если в одном из чисел нет запятой, то считать цифры только в одном числе.

Пример №4. Запись выполнена так, что цифры по правому краю записаны ровно одна под одной, то есть как при обычном умножении чисел в столбик. Умножение выполнено без учета запятой. В ответе справа отделены 4 цифры запятой, так как в первом множителе их 3 после запятой, а во втором – одна, в двух множителях вместе – четыре.

0,125 × 2,3 00375 0250 0,2875

Пример №5. Здесь показано умножение десятичной дроби и целого числа. Умножение выполнено без учета запятой. В ответе отделена справа запятой только одна цифра, так как только в первом множителе есть десятичная часть с одной цифрой после запятой.

Умножение десятичных дробей на 10, 100, 1000…

Чтобы умножить десятичную дробь на 10, 100, 1000 и так далее, нужно перенести запятую вправо на столько цифр, сколько нулей у множителя. Умножение в данном случае выполняется в строчку.

Пример №6. 2,456 × 10 = 24,56 Запятую в десятичной дроби перенесли вправо на 1 цифру, так как у 10 один нуль.

Пример №7. 0,45678 × 100 = 45,678 Запятую перенесли вправо на 2 цифры, так как у 100 два нуля. Нуль, стоящий в начале десятичной дроби, убрали, так как впереди целой части, отличной от нуля он не пишется.

Пример №8. 9,46 × 1000 = 9460 в данном случае при переносе запятой на три цифра не хватило одной, поэтому в конце числа приписали нуль, и в ответе получилось целое число.

Умножение десятичной дроби на разрядную единицу 0,1; 0,01; 0,001…

При умножении десятичной дроби на разрядную единицу 0,1; 0,01; 0,001 (и так далее) нужно перенести запятую на столько цифр влево, сколько цифр в данной разрядной единице после запятой. Умножение обычно выполняется в строчку устно.

Пример №9. 983,7821 × 0,01= 9,837821 Переносим запятые влево на 2 цифры, так как в числе 0,01 две цифры после запятой.

Пример №10. 8,7654 × 0,1 = 0,87654 Перенесли на 1 цифру влево, так как в числе 0,1 одна цифра после запятой. В данном случае перед 8 появился нуль, так как при переносе запятой слева цифр не оказалось.

Пример №11. 7,98 × 0,0001 = 0,000798 При переносе влево на 4 цифры не хватило трех, поэтому впереди поставили нули, а также нуль образуется и в целой части.

Деление десятичных дробей

1. При делении десятичной дроби на целое число выполняют сначала деление целой части, а затем десятичной.
2. При делении десятичной дроби на другую десятичную дробь необходимо в делителе убрать запятую, а в делимом передвинуть ее вправо на столько цифр, сколько их в делителе после запятой. Затем выполнить деление на целое число.
3. Есть случаи, когда цифр после запятой при переносе запятой у дроби не хватает. Тогда необходимо дополнить число нулями.

Пример №12. Деление десятичной дроби на целое число. 46,8 : 2 = 23,4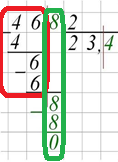

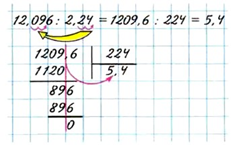
Пример №13. Деление десятичной дроби на десятичную дробь. 12,096 : 2,24 = 5,4 Из данного примера видно, что деление десятичных дробей обязательно сводится к делению на целое число.

Пример №14. 276,3 : 0,003 = 276300 : 3 = 92100. Здесь видно, что не хватает двух цифр в числе 276,3 и поэтому при переносе запятой к нему приписали два нуля. Затем выполнили деление двух целых чисел.

Деление десятичной дроби на 10, 100, 1000…

При делении десятичной дроби на 10,100, 1000 и так далее нужно перенести запятую на столько цифр влево, сколько нулей в данном числе. Деление выполняется в строчку устно.

Пример №16. 134,987 : 1000 = 0,134987 Перенесли запятую на три цифры влево, так как у 1000 три нуля. В целой части поставили нуль, так как цифр не хватило.

Пример №17. 7,234 : 100 = 0,07234 Перенесли запятую влево на две цифры. Так как цифр не хватало, то недостающие заменили нулями.

Деление десятичной дроби на разрядную единицу 0,1; 0,01; 0,001…

При делении десятичной дроби на разрядную единицу 0,1; 0,01; 0,001 и так далее нужно перенести запятую на столько цифр вправо, сколько цифр в данной разрядной единице после запятой. Деление обычно выполняется в строчку устно.

Пример №19. 41,234 : 0,01 = 4123,4 Перенос запятой на 2 цифры вправо, так как в числе 0,01 две цифры после запятой.

Пример №20. 56,91 : 0,001 = 56910 При переносе запятой на три цифры вправо приписали один нуль, так как одной цифры не хватило.

На координатной прямой точки А, В, С и D соответствуют числам -0,201; -0,012; -0,304; 0,021.

Какой точке соответствует число -0,304?

Сформируем из чисел ряд от наименьшего из них до наибольшего. Для этого сначала разделим их на положительные и отрицательные. И сразу получим наибольшее в ряду (поскольку оно единственное больше нуля): 0,021.

Три оставшихся отрицательных распределим по их модулям. Известно, что из двух отрицательных чисел больше то, у которого модуль меньше. Тогда получаем, что –0,304

pазбирался: Даниил Романович | обсудить разбор | оценить

Для получения результата необходимо последовательно выполнить математические действия в соответствии с их приоритетом.

Выполняем возведение в степень. Получаем числа, состоящие из единицы и следующего за ней количества нулей, равного показателю степени. При этом знаки «–» в скобках исчезают, поскольку показатели степеней четные. Получаем:

Выполняем умножение. Для этого в числе 0,3 переносим десятичную запятую на 4 знака вправо (так как в 10000 четыре нуля), а к 4 дописываем, соответственно, 2 нуля. Получаем:

Выполняем сложение –3000+400. Поскольку это числа с разными знаками, то вычитаем из большего модуля меньший и перед результатом ставим «–», поскольку число с большим модулем отрицательное. Получаем:

Так как оба числа отрицательные, то складываем их модули и перед результатом ставим «–». Получаем:

pазбирался: Даниил Романович | обсудить разбор | оценить

Это задание требует простого умения выполнять арифметические действия с десятичными дробями.

Сначала выполняем умножение. Умножаем –13 и –9,3 в столбик без учета знаков «–» перед сомножителями. В полученном произведении отделяем одну – последнюю – цифру десятичной запятой:

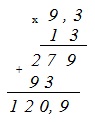
Знак произведения будет положительным, поскольку умножаются два отрицательных числа. Получаем:

Эту разность можно вычислить в столбик, но можно и устно. Выполним это действие в уме: вычитаем отдельно целые части и десятичные. Получаем:

pазбирался: Даниил Романович | обсудить разбор | оценить

Задачу можно решать разными путями, а именно менять последовательность действий, но этот вариант решения рекомендуется для тех, кто уверен в своих возможностях и знает математику на отлично. Для остальных мы рекомендуем выполнить последовательно действия в числителе и знаменателе, а затем разделить числитель на знаменатель. Числитель вычислять в данном примере нет необходимости, это число 9.

Вычислим значение знаменателя:

Можно произвести вычисления в столбик, тогда получим:

Либо перевести дробь к простому виду:

4,5 • 2,5 = 4½ • 2 ½ = 9 / 2 • 5 / 2 = 45 / 4

Последний случай предпочтительней, так как для дальнейшей операции – деления числителя на знаменатель задача упрощается. Делим числитель на знаменатель, умножая числитель на перевернутую дробь в знаменателе:

9 / ( 45 / 4 ) = ( 9 / 1 ) • ( 4 / 45 ) = ( 9 • 4 ) / (1 • 45 )

9 и 45 можно сократить на 9:

( 9 • 4 ) / (1 • 45 ) = ( 1 • 4 )/ (1 • 5 ) = 4 / 5 = 8 / 10 = 0,8

pазбирался: Даниил Романович | обсудить разбор | оценить

Источник статьи: http://spadilo.ru/desyatichnye-drobi/

Напишите цифрами десятичную дробь : одна целая три сотых, одна целая три тысячных?

Русский язык | 10 – 11 классы

Напишите цифрами десятичную дробь : одна целая три сотых, одна целая три тысячных.

Нуль целых одиннадцать сотых, одна целая пять сотых, десять целых восемь сотых.

Пять целых сорок семь тысячных, сорок целых сто пять тысячных, двадцать целых две тысячные.

Нуль целых сто тридцать семь десятитысячных, десять целых пятнадцать стотысячных.

1, 031, 0030, 111, 0510, 085, 04740, 10520, 0020, 013710, 00015.

1, 03 ; 1, 003, 0, 11 ; 1, 05 ; 10, 08.

5, 048 ; 40, 105 ; 20, 002 ; 0, 0137 ; 10, 00015.

Просклонять пятьсот десять целых семьдесят три сотых?

Просклонять пятьсот десять целых семьдесят три сотых.

Проверте написание числа прописью 0?

Проверте написание числа прописью 0.

0021 Ноль целых ноль тысячных ноль сотых двадцать один?

Просклоняйте по падежам : одиннадцать целых тридцать пять сотых, тринадцать целых сорок семь сотых?

Просклоняйте по падежам : одиннадцать целых тридцать пять сотых, тринадцать целых сорок семь сотых.

Помогите пожалуйста, осталось только это.

К семнадцать целых девяносто девять сто пятьдесят шестых прибавить шестнадцать восемнадцатых?

К семнадцать целых девяносто девять сто пятьдесят шестых прибавить шестнадцать восемнадцатых.

К ста сорока четырем целых двадцать три шестьдесят седьмым прибавить пятнадцать третих.

Ноль целых шестьдесят три сотых прибавить тринадцать тринадцатых.

Пожалуйста напишете правильно.

Запишите кооичественные числительные, распределяя их на три группы : а) числительные, обозначающие целые числа ; б) дробные числительные ; в) собирательные числительные?

Запишите кооичественные числительные, распределяя их на три группы : а) числительные, обозначающие целые числа ; б) дробные числительные ; в) собирательные числительные.

Дополните каждую группу тремя примерами.

Два, пятьдесят, пятеро, одна восьмая, пять целых одна десятая, двести, одиннадцать, трое, три четвёртых, шестеро, двадцать пять, оба, одна целая девять сотых, восемь миллионов.

Написать число прописью 0?

Написать число прописью 0.

Ноль целых ноль тысячных ноль сотых двадцать один?

Проверте правильно ли написала, спасибо.

Правильно прочитайте и запишите одна третья пять седьмых двадцать семь целых шесть десятых одна целая восемь десятых?

Правильно прочитайте и запишите одна третья пять седьмых двадцать семь целых шесть десятых одна целая восемь десятых.

Как правильно написать, 30, 7 , тридцать целых семь десятых или семь сотых ?

Как правильно написать, 30, 7 , тридцать целых семь десятых или семь сотых ?

Просклонять по падежам числительные две целых одна третья, десять целых три седьмых, одиннадцать целых пятнадцать сороковых?

Просклонять по падежам числительные две целых одна третья, десять целых три седьмых, одиннадцать целых пятнадцать сороковых.

Как правильно пишется – шестисот целых и двадцать сотых?

Как правильно пишется – шестисот целых и двадцать сотых?

На этой странице сайта размещен вопрос Напишите цифрами десятичную дробь : одна целая три сотых, одна целая три тысячных? из категории Русский язык с правильным ответом на него. Уровень сложности вопроса соответствует знаниям учеников 10 – 11 классов. Здесь же находятся ответы по заданному поиску, которые вы найдете с помощью автоматической системы. Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по заданной теме. На этой странице можно обсудить все варианты ответов с другими пользователями сайта и получить от них наиболее полную подсказку.

Набережная существительное одной чертой(какая) красивая двумя чертами Около подчеркиваем волнистой линией в. В сл моря одна черта существительное Время дня одной чертой сущ какое жаркое двумя чертами ветвями какими большими.

А) парочку Б) дразнится В) стишок.

1 схема. Солнце светит. Повествовательное. 2 схема. Девочка делает зарядку. Повествовательное. 3 схема. С дерева упало сочное яблоко. Повествовательное. 4схема. Мальчик думает о маме и о папе. Повествовательное. 5схема. Крпсивый лебедь п..

Жила – была бедная старушка. Такая она была бедная, что порой ей даже не из чего было хлеба испечь. И была у неё соседка – злыдня, которая эту старушку непрестанно бедностью её попрекала. И вдруг заметила соседка : как только она принимается хлеб ..

1. Звуки речи 2. Сами звуки 1. Песня 2. Басня 3. Конец.

Розы – существительное , укрывают – глагол , на – предлог, зиму – существительное , потому – наречие , что – наречие , побеги – существительное , непокрытая – прилагательное , снегом – существительное , обмерзают – глагол , при – предлог , низких – п..

Начнем с главных членов предложения. 1) Хорош лес 2) окрашена листва 3) расстилаются листья 4) видны шляпки а теперь определение и дополнение. Дополнение(сущ. ) – 1) дни, 2) цвет, 3) – , 4) – . Определение(в данном случае это прилагательные) – 1)..

ПрЕломление ПрЕподнести ПрЕкратить споры ПрЕстиж ПрЕзумция ПрЕмьера ПрЕвратно понятый ПрЕсимпатичный ПрЕсимпатичный.

Решение в приложении Всё остальное у Вас правильно.

Раз – вед – чи – ки | р а с в * э ч * и к * и | 4 слога р (р) согл. , зв. Непарн. , тв. Непарн. , а (а) глас. , безуд. , з (с) согл. , глух. Парн. , тв. Парн. , в (в) согл. , зв. Парн. , мягк. Парн. , е (э) глас. , уд. , д ч(ч) сог..

Источник статьи: http://russkij-azyk.my-dict.ru/q/428371_napisite-ciframi-desaticnuu-drob-odna-celaa/

Что такое десятые и сотые доли?

Что такое десятые и сотые доли? Десятая — это разряд, который представляет позицию цифры после запятой, равную 1/10, а сотая представляет позицию цифры в числе после запятой, равную 1/100.. Например, девять десятых равны 9/10 = 0.9, а 5 сотых равны 5/100 = 0.05.

Точно так же какое число находится в одной десятой числа 29.4 5? следовательно, мы можем сделать вывод, что, 4 находится на одной десятой в числе 29.45 .

Какое значение равно 5 сотым? 5 сотых (5 х 0.01)

Похожие страницы:Блог

Какие есть 3 вида налогов?

Как найти среднюю точку между двумя точками?

Как вы делаете кадровые прогнозы?

Как найти начальную скорость, зная только время?

Числовое слово для 0.65 составляет шестьдесят пять сотых и совпадает с его числовым значением. Это потому, что число 65 находится справа от десятичной точки, указывая на десятичную дробь в сотых долях.

Как считать десятками? Мы можем считать в десятых по увеличение числа в верхней части дроби. Число внизу этих дробей говорит нам, сколько десятых у нас есть. По мере увеличения числа мы добавляем еще одну десятую. 10 десятых записывается как 10 / ₁₀ , что составляет одно целое.

Во-вторых, сколько десятых в числе 2? Итак, два целых числа — это сколько десятых? Ну, целое равно 10 десятым, значит, два целых равны 20 десятых. Так что я мог написать двойку, переписать двойку как 20 десятых.

Какое место занимает сотый?

Вторая цифра справа от десятичной точки указывает количество сотых.

тогда что такое сотые в десятичных дробях? Числа с разрядным значением

Когда мы пишем числа с сотыми долями, используя десятичные дроби, мы используем десятичную точку и разряды справа от нее. Сотое место два разряда справа от десятичной точки. 73/100 = 73. .

Что такое 8 сотых в виде десятичной дроби?

Что такое десятые в математике?

Главная > Математическая лексика > Десятки. Первая цифра справа от десятичной точки; одна из 10 равных частей целого.

Как написать шесть десятых в сотых? Разделите число десятых на 0.1, чтобы преобразовать в сотые. Например, если у вас есть 6 десятых, разделите 6 на 0.1, чтобы получить 60 сотых. Умножьте число десятых на 10, чтобы перевести в сотые. Проверив ответ, умножьте 6 на 10, чтобы получить 60 сотых.

Дробь две десятых, или 2/10, может быть записана как десятичная дробь. 0.2.

Как считать в сотых? Тис ты делишь целое на 100 равных частей, каждая часть равна сотой ( 1⁄100 ). Вы также можете получить 1/100, разделив десятую часть (1/10) на 10 меньших частей.

Что такое десятые доли в десятичных дробях?

Если в числе есть десятичная точка, то первая цифра справа от десятичной точки указывает количество десятых долей. Например, десятичная дробь 0.3 совпадает с дробью 310. Вторая цифра справа от десятичной точки указывает количество сотых.

Как вычислить 3 десятых числа?

3/10 равно 0.3. Напишите число без десятичной дроби, которое будет равно 3. Напишите «x 10^-1» после 3, потому что десятичная дробь находится на одну позицию левее 3. Полный ответ будет выглядеть как «3 х 10 ^ -1“.

Сколько десятых в числе 6? цифра 6 стоит на десятом месте, ее значение равно 6 × 0.1 или 0.6.

Как написать четыре десятых? 4/10 как десятичная 0.4.

Как написать 9 десятых?

9/10 (девять десятых), записанные в виде десятичной дроби, 0.9 (ноль целых девять десятых).

Что такое пример значения в математике? В математике ценность – это число, обозначающее результат вычисления или функции. Итак, в приведенном выше примере вы можете сказать своему учителю, что значение 5 x 6 равно 30 или значение x + y, если x = 6 и y = 3, равно 9. Значение также может относиться к переменной или константе. … Общие переменные — это x или y.

Какая цифра стоит на десятом месте?

Цифра на десятом месте первая цифра справа от запятой.

Где ближайшее сотое место? Ближайшая сотая вторая цифра после десятичной точки.

Как читать сотые?

Что такое сотая в математике? сотая часть, особенно одна (1/100). …Также называется сотой. (в десятичной системе счисления) положение второй цифры справа от запятой.

Источник статьи: http://reviews.tn/ru/wiki/what-are-tenths-and-hundredths/

Десятичные дроби – для чайников

Действия с десятичными дробями – деление умножение, сложение, вычитание, сравнение. Разбор примеров.

Между прочим, большинство ошибок на экзаменах происходят как раз из-за незнания простейших действий вроде этих.

Так что читай эту статью и отрабатывай скиллы.

Десятичные дроби – коротко о главном

1. Определение

Десятичной дробью называется обыкновенная дробь, знаменателем которой является \( 10\) в какой-либо степени.

2. Конечная и бесконечная десятичная дробь

Десятичная дробь может быть:

• конечной, если она содержит конечное число цифр после запятой (\( \displaystyle \frac<8><10>,\ \frac<13><100>,\frac<49><1000>\));
• бесконечной, в том числе периодичной, если конечное число цифр определить не определено (\( 0,05882352941…\));
• периодической, если её последовательность цифр после запятой, начиная с некоторого места, представляет собой периодически повторяющуюся группу цифр (\( \displaystyle \frac<1><7>=0,\underbrace<142857>_<<период>>\underbrace<142857>_<период>142…=0,\left( 142857 \right)\))

3. Свойства десятичных дробей

• Десятичная дробь не меняется, если справа добавить нули \( \displaystyle \frac<3><100>=0,03=0,030=0,030000\)и т.д.;
• Десятичная дробь не меняется, если удалить нули, расположенные в конце десятичной дроби: \( 0,014330000=0,01433\);
• Десятичная дробь возрастает в \( 10\), \( 100\), \( 1000\) и т.д. раз, если перенести десятичную точку на одну, две, три и т.д. позиций вправо: \( 0,0125\cdot 100=1,25\) (перенесли запятую на \( 2\) знака вправо – умножили на \( 100\) и дробь возросла в \( 100\) раз);
• Десятичная дробь уменьшается в \( 10\), \( 100\), \( 1000\) и т.д. раз, если перенести десятичную точку на одну, две, три и т.д. позиций влево: \( 124,56:100=1,2456\) (перенесли запятую на \( 2\) знака влево – разделили на \( 100\) и дробь уменьшилась в \( 100\) раз).

4. Сложение десятичных дробей

Сложение происходит, как и сложение натуральных чисел в столбик, при этом запятая в ответе ставиться четко на том же месте, как и в складываемых числах.

5. Вычитание десятичных дробей

Так же, как и при сложении, при вычитании десятичные дроби записываются «столбиком»:

6. Умножение десятичных дробей

Десятичные дроби также записываются в столбик и умножаются как обыкновенные числа. При умножении нам неважно, стоят ли запятые под запятыми и так далее.

Однако, удобно, когда числа выровнены по правому краю – умножение происходит более упорядочено.

7. Деление десятичных дробей

Деление десятичной дроби на натуральное число

• Делим десятичную дробь на натуральное число по правилам деления в столбик, не обращая внимания на запятую в делимом (то число, которое мы делим на какое-либо другое число)
• Ставим в частном запятую, когда заканчивается деление целой части делимого.

Деление десятичных дробей друг на друга

• Считаем количество знаков справа от запятой в десятичной дроби.
• Умножаем и делимое, и делитель на 10, 100 или 1000 и т.д., в зависимости от того, сколько мы насчитали знаков в первом пункте. Умножать необходимо, чтобы превратить десятичную дробь в целое число.

Десятичные дроби – подробнее

Конечно, ты знаешь, что такое обыкновенная дробь. Например, \( \displaystyle \frac<1><3>,\ \frac<1><4>,\frac<5><112>\).

Наравне с приведенными выше дробями существуют дроби \( \displaystyle \frac<8><10>,\ \frac<13><100>,\frac<49><1000>\) и т.д.

Такие дроби можно записать намного удобнее и более кратко, то есть:

Данного вида дроби называются десятичными. Иными словами:

Десятичной дробью называется обыкновенная дробь, знаменателем которой является \( 10\) в какой-либо степени (первый пример – \( 10\) в первой степени, второй – \( 10\) во второй степени и т.д.).

Ты наверняка знаешь, что каждая цифра после запятой имеет свое название. На всякий случай напомню тебе про них, чтобы в дальнейшем мы говорили на одном языке:

Это огромное число читается по следующему алгоритму:

1. Сначала читается число, стоящее до запятой и добавляется слово «целых»: ««\( 46\) целых»;
2. Затем читается как обыкновенное число слева после запятой и добавляется слово, обозначающее название самой последней цифры. В нашем случае – «одна тысяча двести тридцать четыре десятитысячные».

А теперь прочитаем все вместе – «\( 46\) целых одна тысяча двести тридцать четыре десятитысячные». Разобрался? Переходим к визуализации полученных знаний!

Итак, небольшая тренировка на понимание, что такое эта десятичная дробь! Нарисуй квадрат \( 10\) на \( 10\) и закрась какую-нибудь его часть равную:

Справился? Проверяем, что у тебя получилось.

Во-первых, квадрат \( 10\) на \( 10\) состоит из \( 100\) клеточек. Соответственно, \( 0.05\) – \( 5\) клеточек из \( 100\); \( 0,4\) – \( 40\) клеточек из \( 100\) и так далее.

Наверняка, наибольшее затруднение составило последнее число – \( -0,245\). На картинке это необходимо отразить как 24,5 клетки.

С понятиями разобрались, теперь научимся переводить из десятичной дроби в обыкновенную и обратно.

Перевод из десятичной дроби в обыкновенную и обратно

Уверена, что ты с легкостью справился! А как насчет обратного перевода? Из обыкновенных в десятичные?

Попробуй свои силы на вот этих дробях:

Если ты со всем справился, можешь пропускать следующий абзац, а если где-то допустил ошибку, внимательно прочти о том, как легко и 100% правильно переводить дроби из обыкновенных в десятичные.

1. Смотрим на дробь и определяем, есть ли у нее целая часть? Если есть, выделяем целую часть, записываем ее, и ставим запятую.
2. После запятой должно быть столько знаков, сколько нулей стоит в знаменателе. Например, дробь \( \displaystyle \frac<4><1000>\) – \( 3\) нуля в знаменателе, соответственно, мы как бы мысленно выделяем \( 3\) ячейки.
3. Затем записываем числитель – \( 4\), но выравниваем его по правому краю, а в пустые ячейки вставляем нули.

Разобрался? Посмотри еще раз эту маленькую «инструкцию»:

Я думаю, ты во всем-всем разобрался! Потренируемся? Попробуй поработать еще с вот этими дробями:

Виды десятичных дробей

Десятичная дробь может быть:

• конечной, если она содержит конечное число цифр после запятой (\( \displaystyle \frac<8><10>,\ \frac<13><100>,\frac<49><1000>\));
• бесконечной, в том числе периодичной, если конечное число цифр определить не определено (\( 0,05882352941…\));
• периодической, если её последовательность цифр после запятой, начиная с некоторого места, представляет собой периодически повторяющуюся группу цифр (\( \displaystyle \frac<1><7>=0,\underbrace<142857>_<<период>>\underbrace<142857>_<период>142…=0,\left( 142857 \right)\)).

Поговорим сначала о конечных дробях.

Конечная десятичная дробь

Само собой понятно, что дроби \( \displaystyle \frac<8><10>,\ \frac<13><100>,\frac<49><1000>\) являются конечными, ведь знаменатель дроби уже представлен как единица с последующими нулями, и поэтому мы сразу можем сказать, что данную обыкновенную дробь можно перевести в конечную десятичную. А что ты скажешь насчет этой дроби: \( \displaystyle \frac<1><4>\)? Ее знаменатель далеко не единица с последующими нулями, но ты четко знаешь, что у нее есть десятичный «аналог»:

То есть, чтобы определить, можно ли перевести дробь в десятичную, необходимо умножить числитель и знаменатель на одно и то же число, такое, чтобы знаменатель стал равен \( 10\), \( 100\), \( 1000\) и так далее.

Усвоил? Постарайся представить в виде конечной десятичной дроби следующие обыкновенные дроби:

Справился? Молодец. Выходим на новый уровень и переходим к бесконечным десятичным дробям.

Бесконечная десятичная дробь

Итак, бери калькулятор и дели \( 1\) на \( 17\). Поделил? Ты получил \( 0,05882352941\) и дальше окошко калькулятора не показывает… Это тоже является десятичной дробью, только данная десятичная дробь является бесконечной. Ты сейчас скажешь, а как же наше определение?

Десятичной дробью называется обыкновенная дробь, знаменателем которой является \( 10\) в какой-либо степени (первый пример – \( 10\) в первой степени, второй – \( 10\) во второй степени и т.д.).

Все очень просто и никаких противоречий с определением нет. В данном случае нам необходимо привести наш знаменатель к \( <<10>^>\), с учетом, что \( n\) это какое-либо бесконечное число, которое мы не можем «обозреть» взглядом», или иными словами – \( n\to +\infty \)

Бесконечной десятичной дробью называется обыкновенная дробь, в записи которой после запятой содержится бесконечное количество цифр.

Как правило, в задачах, где встречаются бесконечные десятичные дроби, просят указать ответ либо с округлением (например, до десятых, или до сотых), либо записать в виде обыкновенной дроби, то есть как \( \displaystyle \frac<1><17>\).

Подумай, какой самый популярный пример можно привести на тему «бесконечная десятичная дробь»? Правильно! Число \( \pi \) является бесконечной десятичной дробью. Во всем мире люди договорились, что для решения математических задач принято, что \( \pi =3,14\), но это далеко не так. Число \( \pi \) не имеет определенного завершения. Оно настолько бесконечно, что ежегодно в мире проводятся соревнования по запоминанию числа \( \pi \). Мировой рекорд по запоминанию знаков числа \( \pi \) после запятой принадлежит китайцу Лю Чао, который в 2006 году в течение 24 часов и 4 минут воспроизвёл 67 890 знаков после запятой без ошибки! Все 67 890 знаков после запятой мы приводить не будем, а приведем несколько сокращенную запись:

Думаю, этого хватит, чтобы оценить «масштабы» данного числа.

Наравне с бесконечными десятичными дробями существуют периодические десятичные дроби. Они так же не имеют конца, но последующие числа в них повторяются, например, попробуй перевести в десятичную дробь \( \displaystyle \frac<1><3>\). Что у тебя получилось?

Чтобы не повторять число \( 3\) много много раз, решили говорить «ноль целых и три в периоде», так как тройка будет повторяться после запятой бесконечное число раз. Из этого умозаключения следует определение:

Дробь называется периодической, если её последовательность цифр после запятой, начиная с некоторого места, представляет собой периодически повторяющуюся группу цифр.

Чтобы кратко записать такую дробь, период (повторяющиеся цифры после запятой) пишут в скобках:

\( \displaystyle \frac<1><3>=0,\underbrace<3>_<период>33333333….=0,\left( 3 \right)\)

\( \displaystyle \frac<1><7>=0,\underbrace<142857>_<<период>>\underbrace<142857>_<период>142…=0,\left( 142857 \right)\)

Важно, что период не может начинаться слева от запятой:

\( \displaystyle \frac<100><7>=\underbrace<14,2857>_<не период>1428571428571…=14,\left( 285714 \right)\).

Источник статьи: http://youclever.org/book/desyatichnye-drobi-1/

Десятичные дроби | теория по математике 🎲 числа и вычисления

Десятичная дробь — дробь, которая представляет собой способ представление числа в виде записи числа с запятой, где цифры перед запятой называются целой частью, а цифры после запятой – дробной частью (десятичной частью).

Десятичные дроби получают из записи обыкновенных дробей со знаменателем 10, 100, 1000 и так далее. Например, десятичные дроби:

4,56 – четыре целых пятьдесят шесть сотых 18,234 – восемнадцать целых двести тридцать четыре тысячных 78,6 – семьдесят восемь целых шесть десятых

Чтение десятичной части (десятых, сотых и так далее) зависит от количества цифр после запятой. Если цифра одна, то читают – десятых (в числе десять – один нуль, это соответствует одной цифре). Если две цифры после запятой, то читают – сотых (в сотне два нуля).

Десятичные дроби получаются из обыкновенных дробей: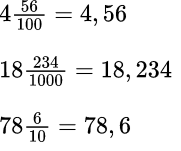

Сложение (вычитание) десятичных дробей

1. Записать их друг под другом так, чтобы при записи запятая оказалась под запятой и соответствующий разряд под соответствующим.
2. Уравнять количество знаков после запятой, добавляя недостающие нулями.
3. Выполнить сложение (вычитание) в столбик, не обращая внимания на запятую.
4. Поставить запятую под запятыми.

Если складывают (вычитают) целое число и десятичную дробь, то нужно поставить запятую после целого числа и приписать необходимое количество нулей после запятой.

Пример №1. Запись, где запятая под запятой и соответствующий разряд под соответствующим.

Пример №2. Запись, где также запятая под запятой, а во втором числе дописан нуль, чтобы уравнять количество знаков после запятой.

Пример №3. В первом слагаемом нет десятичной части, поэтому, после числа 56 поставили запятую и добавили нужное количество нулей.

Умножение десятичных дробей

При умножении двух десятичных дробей в столбик необходимо:

1. Написать числа одно под другим, не обращая внимания на запятую
2. Выполнить умножение в столбик
3. В ответе отделить столько цифр справа запятой, сколько их в обоих множителях вместе. Если в одном из чисел нет запятой, то считать цифры только в одном числе.

Пример №4. Запись выполнена так, что цифры по правому краю записаны ровно одна под одной, то есть как при обычном умножении чисел в столбик. Умножение выполнено без учета запятой. В ответе справа отделены 4 цифры запятой, так как в первом множителе их 3 после запятой, а во втором – одна, в двух множителях вместе – четыре.

0,125 × 2,3 00375 0250 0,2875

Пример №5. Здесь показано умножение десятичной дроби и целого числа. Умножение выполнено без учета запятой. В ответе отделена справа запятой только одна цифра, так как только в первом множителе есть десятичная часть с одной цифрой после запятой.

Умножение десятичных дробей на 10, 100, 1000…

Чтобы умножить десятичную дробь на 10, 100, 1000 и так далее, нужно перенести запятую вправо на столько цифр, сколько нулей у множителя. Умножение в данном случае выполняется в строчку.

Пример №6. 2,456 × 10 = 24,56 Запятую в десятичной дроби перенесли вправо на 1 цифру, так как у 10 один нуль.

Пример №7. 0,45678 × 100 = 45,678 Запятую перенесли вправо на 2 цифры, так как у 100 два нуля. Нуль, стоящий в начале десятичной дроби, убрали, так как впереди целой части, отличной от нуля он не пишется.

Пример №8. 9,46 × 1000 = 9460 в данном случае при переносе запятой на три цифра не хватило одной, поэтому в конце числа приписали нуль, и в ответе получилось целое число.

Умножение десятичной дроби на разрядную единицу 0,1; 0,01; 0,001…

При умножении десятичной дроби на разрядную единицу 0,1; 0,01; 0,001 (и так далее) нужно перенести запятую на столько цифр влево, сколько цифр в данной разрядной единице после запятой. Умножение обычно выполняется в строчку устно.

Пример №9. 983,7821 × 0,01= 9,837821 Переносим запятые влево на 2 цифры, так как в числе 0,01 две цифры после запятой.

Пример №10. 8,7654 × 0,1 = 0,87654 Перенесли на 1 цифру влево, так как в числе 0,1 одна цифра после запятой. В данном случае перед 8 появился нуль, так как при переносе запятой слева цифр не оказалось.

Пример №11. 7,98 × 0,0001 = 0,000798 При переносе влево на 4 цифры не хватило трех, поэтому впереди поставили нули, а также нуль образуется и в целой части.

Деление десятичных дробей

1. При делении десятичной дроби на целое число выполняют сначала деление целой части, а затем десятичной.
2. При делении десятичной дроби на другую десятичную дробь необходимо в делителе убрать запятую, а в делимом передвинуть ее вправо на столько цифр, сколько их в делителе после запятой. Затем выполнить деление на целое число.
3. Есть случаи, когда цифр после запятой при переносе запятой у дроби не хватает. Тогда необходимо дополнить число нулями.

Пример №12. Деление десятичной дроби на целое число. 46,8 : 2 = 23,4

Пример №13. Деление десятичной дроби на десятичную дробь. 12,096 : 2,24 = 5,4 Из данного примера видно, что деление десятичных дробей обязательно сводится к делению на целое число.

Пример №14. 276,3 : 0,003 = 276300 : 3 = 92100. Здесь видно, что не хватает двух цифр в числе 276,3 и поэтому при переносе запятой к нему приписали два нуля. Затем выполнили деление двух целых чисел.

Деление десятичной дроби на 10, 100, 1000…

При делении десятичной дроби на 10,100, 1000 и так далее нужно перенести запятую на столько цифр влево, сколько нулей в данном числе. Деление выполняется в строчку устно.

Пример №16. 134,987 : 1000 = 0,134987 Перенесли запятую на три цифры влево, так как у 1000 три нуля. В целой части поставили нуль, так как цифр не хватило.

Пример №17. 7,234 : 100 = 0,07234 Перенесли запятую влево на две цифры. Так как цифр не хватало, то недостающие заменили нулями.

Деление десятичной дроби на разрядную единицу 0,1; 0,01; 0,001…

При делении десятичной дроби на разрядную единицу 0,1; 0,01; 0,001 и так далее нужно перенести запятую на столько цифр вправо, сколько цифр в данной разрядной единице после запятой. Деление обычно выполняется в строчку устно.

Пример №19. 41,234 : 0,01 = 4123,4 Перенос запятой на 2 цифры вправо, так как в числе 0,01 две цифры после запятой.

Пример №20. 56,91 : 0,001 = 56910 При переносе запятой на три цифры вправо приписали один нуль, так как одной цифры не хватило.

На координатной прямой точки А, В, С и D соответствуют числам -0,201; -0,012; -0,304; 0,021.

Какой точке соответствует число -0,304?

Сформируем из чисел ряд от наименьшего из них до наибольшего. Для этого сначала разделим их на положительные и отрицательные. И сразу получим наибольшее в ряду (поскольку оно единственное больше нуля): 0,021.

Три оставшихся отрицательных распределим по их модулям. Известно, что из двух отрицательных чисел больше то, у которого модуль меньше. Тогда получаем, что –0,304

pазбирался: Даниил Романович | обсудить разбор | оценить

Для получения результата необходимо последовательно выполнить математические действия в соответствии с их приоритетом.

Выполняем возведение в степень. Получаем числа, состоящие из единицы и следующего за ней количества нулей, равного показателю степени. При этом знаки «–» в скобках исчезают, поскольку показатели степеней четные. Получаем:

Выполняем умножение. Для этого в числе 0,3 переносим десятичную запятую на 4 знака вправо (так как в 10000 четыре нуля), а к 4 дописываем, соответственно, 2 нуля. Получаем:

Выполняем сложение –3000+400. Поскольку это числа с разными знаками, то вычитаем из большего модуля меньший и перед результатом ставим «–», поскольку число с большим модулем отрицательное. Получаем:

Так как оба числа отрицательные, то складываем их модули и перед результатом ставим «–». Получаем:

pазбирался: Даниил Романович | обсудить разбор | оценить

Это задание требует простого умения выполнять арифметические действия с десятичными дробями.

Сначала выполняем умножение. Умножаем –13 и –9,3 в столбик без учета знаков «–» перед сомножителями. В полученном произведении отделяем одну – последнюю – цифру десятичной запятой:

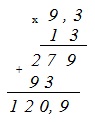
Знак произведения будет положительным, поскольку умножаются два отрицательных числа. Получаем:

Эту разность можно вычислить в столбик, но можно и устно. Выполним это действие в уме: вычитаем отдельно целые части и десятичные. Получаем:

pазбирался: Даниил Романович | обсудить разбор | оценить

Задачу можно решать разными путями, а именно менять последовательность действий, но этот вариант решения рекомендуется для тех, кто уверен в своих возможностях и знает математику на отлично. Для остальных мы рекомендуем выполнить последовательно действия в числителе и знаменателе, а затем разделить числитель на знаменатель. Числитель вычислять в данном примере нет необходимости, это число 9.

Вычислим значение знаменателя:

Можно произвести вычисления в столбик, тогда получим:

Либо перевести дробь к простому виду:

4,5 • 2,5 = 4½ • 2 ½ = 9 / 2 • 5 / 2 = 45 / 4

Последний случай предпочтительней, так как для дальнейшей операции – деления числителя на знаменатель задача упрощается. Делим числитель на знаменатель, умножая числитель на перевернутую дробь в знаменателе:

9 / ( 45 / 4 ) = ( 9 / 1 ) • ( 4 / 45 ) = ( 9 • 4 ) / (1 • 45 )

9 и 45 можно сократить на 9:

( 9 • 4 ) / (1 • 45 ) = ( 1 • 4 )/ (1 • 5 ) = 4 / 5 = 8 / 10 = 0,8

pазбирался: Даниил Романович | обсудить разбор | оценить

Источник статьи: http://spadilo.ru/desyatichnye-drobi/

Что такое десятые и сотые доли?

Что такое десятые и сотые доли? Десятая — это разряд, который представляет позицию цифры после запятой, равную 1/10, а сотая представляет позицию цифры в числе после запятой, равную 1/100.. Например, девять десятых равны 9/10 = 0.9, а 5 сотых равны 5/100 = 0.05.

Точно так же какое число находится в одной десятой числа 29.4 5? следовательно, мы можем сделать вывод, что, 4 находится на одной десятой в числе 29.45 .

Какое значение равно 5 сотым? 5 сотых (5 х 0.01)

Похожие страницы:Блог

Какие есть 3 вида налогов?

Как найти среднюю точку между двумя точками?

Как вы делаете кадровые прогнозы?

Как найти начальную скорость, зная только время?

Числовое слово для 0.65 составляет шестьдесят пять сотых и совпадает с его числовым значением. Это потому, что число 65 находится справа от десятичной точки, указывая на десятичную дробь в сотых долях.

Как считать десятками? Мы можем считать в десятых по увеличение числа в верхней части дроби. Число внизу этих дробей говорит нам, сколько десятых у нас есть. По мере увеличения числа мы добавляем еще одну десятую. 10 десятых записывается как 10 / ₁₀ , что составляет одно целое.

Во-вторых, сколько десятых в числе 2? Итак, два целых числа — это сколько десятых? Ну, целое равно 10 десятым, значит, два целых равны 20 десятых. Так что я мог написать двойку, переписать двойку как 20 десятых.

Какое место занимает сотый?

Вторая цифра справа от десятичной точки указывает количество сотых.

тогда что такое сотые в десятичных дробях? Числа с разрядным значением

Когда мы пишем числа с сотыми долями, используя десятичные дроби, мы используем десятичную точку и разряды справа от нее. Сотое место два разряда справа от десятичной точки. 73/100 = 73. .

Что такое 8 сотых в виде десятичной дроби?

Что такое десятые в математике?

Главная > Математическая лексика > Десятки. Первая цифра справа от десятичной точки; одна из 10 равных частей целого.

Как написать шесть десятых в сотых? Разделите число десятых на 0.1, чтобы преобразовать в сотые. Например, если у вас есть 6 десятых, разделите 6 на 0.1, чтобы получить 60 сотых. Умножьте число десятых на 10, чтобы перевести в сотые. Проверив ответ, умножьте 6 на 10, чтобы получить 60 сотых.

Дробь две десятых, или 2/10, может быть записана как десятичная дробь. 0.2.

Как считать в сотых? Тис ты делишь целое на 100 равных частей, каждая часть равна сотой ( 1⁄100 ). Вы также можете получить 1/100, разделив десятую часть (1/10) на 10 меньших частей.

Что такое десятые доли в десятичных дробях?

Если в числе есть десятичная точка, то первая цифра справа от десятичной точки указывает количество десятых долей. Например, десятичная дробь 0.3 совпадает с дробью 310. Вторая цифра справа от десятичной точки указывает количество сотых.

Как вычислить 3 десятых числа?

3/10 равно 0.3. Напишите число без десятичной дроби, которое будет равно 3. Напишите «x 10^-1» после 3, потому что десятичная дробь находится на одну позицию левее 3. Полный ответ будет выглядеть как «3 х 10 ^ -1“.

Сколько десятых в числе 6? цифра 6 стоит на десятом месте, ее значение равно 6 × 0.1 или 0.6.

Как написать четыре десятых? 4/10 как десятичная 0.4.

Как написать 9 десятых?

9/10 (девять десятых), записанные в виде десятичной дроби, 0.9 (ноль целых девять десятых).

Что такое пример значения в математике? В математике ценность – это число, обозначающее результат вычисления или функции. Итак, в приведенном выше примере вы можете сказать своему учителю, что значение 5 x 6 равно 30 или значение x + y, если x = 6 и y = 3, равно 9. Значение также может относиться к переменной или константе. … Общие переменные — это x или y.

Какая цифра стоит на десятом месте?

Цифра на десятом месте первая цифра справа от запятой.

Где ближайшее сотое место? Ближайшая сотая вторая цифра после десятичной точки.

Как читать сотые?

Что такое сотая в математике? сотая часть, особенно одна (1/100). …Также называется сотой. (в десятичной системе счисления) положение второй цифры справа от запятой.

Источник статьи: http://reviews.tn/ru/wiki/what-are-tenths-and-hundredths/